How the ratings are calculated
The actual functions used are available in pdf format.
Players may be loosely classified according to rating by the following scheme:
- over 2300
- grand master
- over 2100
- senior master
- over 1900
- master
- over 1700
- expert
- over 1500
- apprentice
- less than 1500
- novice
The program is designed to give a rating for each player that takes into account performance and the strength (or otherwise) of partners and opponents. The rating is calculated on a tournament-by-tournament basis, and it should be appreciated that the program is a RATINGS system, and not a RANKING system. Earlier algorithms (dating back to the mid-1980's) were fairly successful, but anomalous results would arise in certain cases. The ideal program needs to be flexible enough to cope sensibly with tournaments that have:
- many play-ers or very few players
- many games or very few games
- people playing in their first ever event
- players returning to the game after a long absence
- singles games or pairs games (sometimes both!)
- fixed partnerships (and sometimes fixed opponents) or varying partnerships
It would also be nice if the algorithm had a reasonably firm mathematical basis that avoided making too many arbitrary judgements over the parameters that influence ratings.
The key parameters calculated each tournament for each player are:
- the player's rating
- the player's Rating Reliability Factor (RRF); this provides a measure of the confidence that the program has in that player's rating.
In the new algorithm, an RRF of 100 is equivalent to an estimated uncertainty in the rating of +-70 points, while an RRF of 0 is equivalent to an uncertainty of +-350 rating points. Players who play in most tournaments will eventually gain an RRF of 100, while those who only play a few games a year will have low RRF values.
The adjustment to a player's rating each tournament takes into account:
- the points per game (p.p.g.) achieved.
- the number of games played in the tournament.
- the strength of the partner(s) and opponent(s).
- the initial uncertainty in the player's rating. There will be smaller adjustments for players with low uncertainties compared to those with high uncertainties
- the uncertainties in the ratings of partner(s) and opponent(s); for instance, there will only be small adjustments for players partnering complete beginners (as the beginner has a high uncertainty in rating). Similarly only small adjustments will be made for players partnering someone returning to the game after a long absence.
Prediction of scores
The predicted score in a game of pairs is given by:
PREDICTEDSCORE = 3.5 + 3.55 erf((RATING + PARTNERRATING - OPP1RATING - OPP2RATING)/1600)(subject to the predicted score not being outside the range 0-7). Here "erf" denotes the error function.
Similarly for a game of singles:
PREDICTEDSCORE = 3.5 + 3.55 erf((RATING - OPPRATING)/800)This function is shown in the graph below:
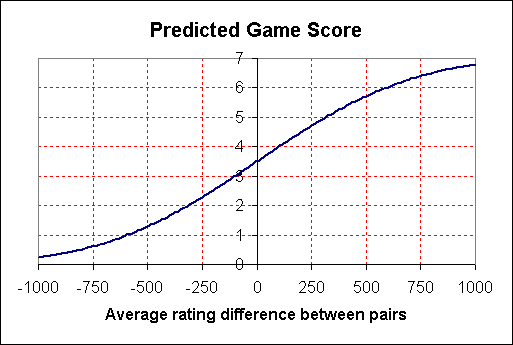
It can be seen that an average ratings points difference between pairs of:
- 100 points predicts a 4-3 win
- 205 points predicts a 4.5-2.5 win
- 315 points predicts a 5-2 win
- 440 points predicts a 5.5-1.5 win
- 590 points predicts a 6-1 win
- 805 points predicts a 6.5-0.5 win
(Incidentally, the ratings may be used to calculate handicaps on the basis of this function).
Calculation of Ratings
The first step in the program is to calculate a tournament rating for each player in the tournament. This is the rating that the player would need to have had in order to be predicted the same number of total points as was actually achieved.
The second step in the program is to calculate the estimated uncertainty in the tournament rating. This has two contributions. One is due to the finite number of games played - effectively each game can be treated as being an independent "measurement" of tournament rating. The second contribution is due to the uncertainties in rating of partner and opponents. These factors can be estimated by appropriate statistical analysis.
At this stage OLDRATING and OLDERROR are known, and the TMTRATING and TMTERROR are known. The new rating is calculated as the best average of two Normally distributed observations with these properties. This is the average of the OLDRATING and TMTRATING weighted by the reciprocal of the square of the uncertainty in these values. The uncertainty (NEWERROR) in the rating is calculated in a similar manner, but the minimum uncertainty is set at 70 rating points.
Tournament newcomers
Tournament newcomers are assigned an initial rating of about 1500, and an uncertainty of 350 rating points. The actual value used depends on whether the rating is being calculated for the newcomer, or whether a tournament rating is being calculated for a player who partnered or opposed the newcomer.
If a calculated rating becomes less than that of a "nominal beginner" (1500 rating points), then a small adjustment to it is made to ensure that the rating never becomes significantly less than a beginner. A lower rating limit of 1320 is chosen. There are no players worse than 1320. An additional small increase in the uncertainty of a player's rating is also made for these players, to allow for the fact that experience shows that people of this quality can show rapid sudden improvements (e.g. if they start practising).
Inactive players
The uncertainty in rating of players who haven't played for a while needs to be increased. No adjustment is made if the player's last tournament was within the previous 4 months. After the 4 month period, a player's uncertainty is increased by 5 SQRT(M-4), where M is the number of months since the last tournament played, whenever ratings are calculated for an open tournament; no uncertainty increase is made for "closed" events such as World Singles and University matches.
Any player not competing in a tournament for over a year is removed from the published ratings. When they next play in a tournament, they will re-enter the ratings at a starting point adjusted slightly from their last rating. Players lapsing with ratings higher than 1500 have their rating adjusted towards 1500 by 15% of the difference (to allow for being "out of practice"), while those with ratings less than 1500 have their ratings adjusted upwards towards 1500 by a factor of 50%.
| Back to the ETwA ratings page. |
|